Transfomation Matrix

Transormation matrix is used to calculate new coordinates of transformed object. By changing values of transformation matrix, it is possible to apply any transformations to objects (scaling, mirroring, rotating, moving etc). Any transformation preserves parallel lines.

Coordinates in PDF are described in 2-dimensional space. Point (x,y) in 2-d space can be described as [x y 1] in vector form. Constant third member of the vector (1) is required for simplicity of calculations with 3×3 matrices, described below.

Transformation between two coordinate systems is described as 3×3 matrix. In matrix form it looks as following:

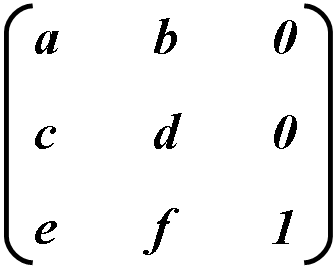
Coordinate transformations are written as cross product:

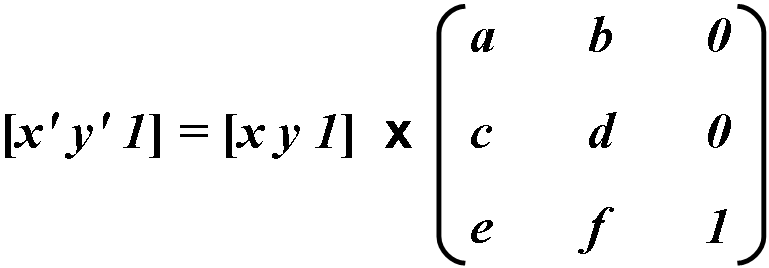
Since last row doesn’t effect calculations result, it is omitted. Transformation coordinates are calculated as follows:

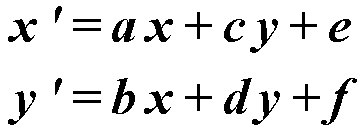
Identity matrix

Identity matrix is one which has a and d values equal to 1 and others equal to 0. This matrix is applied by default since it doesn’t lead to any transformation. This is why it is base for further transformations.

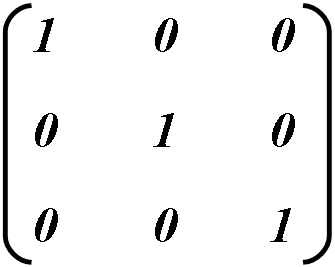
Scaling

To increase object’s horizontal or vertical size value a or d respectively must be changed, other values must stay as in identity matrix.

Example: To increase object’s horizontal size, a value must equal to 2 and other values must stay as in identity matrix. _.

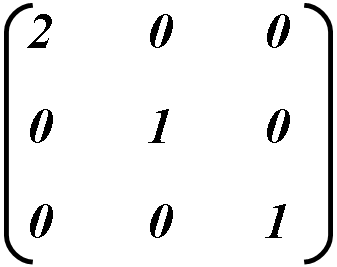
Calculating new object’s coordinates:

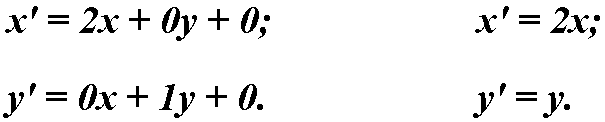
Mirroring

To get horizontal mirroring, it is required to set a = -1, or d = -1 for vertical mirroring. It is possible to change both a and d to get both horizontal and vertical mirroring.

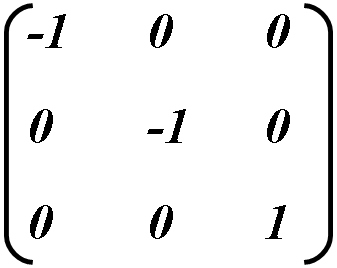
Skew

To vertically or horizontally skew object value b or c respectively must be changed. b/-b is skew up/down, c/-c does left/right skew.

Example: To vertical skew object set b = 1.

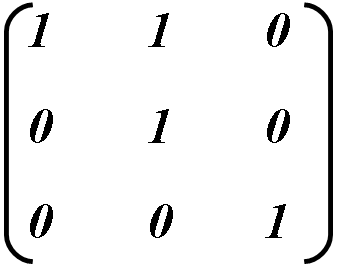
Calculating new object’s coordinates:

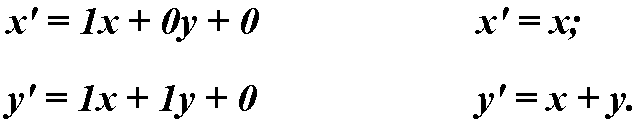
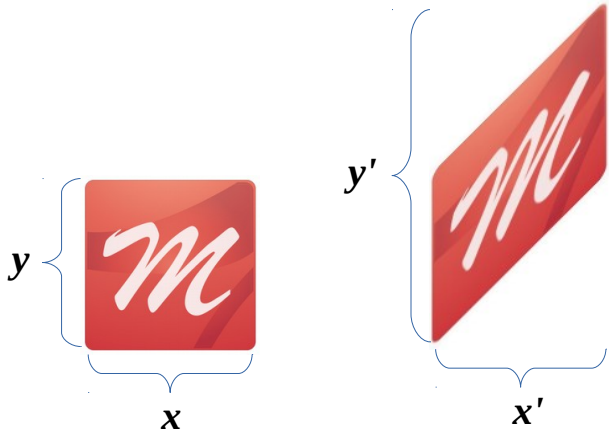
As a result, object is skewed by y coordinate only, which is increased by x.

Rotate

Rotate is a combination of scale and skew, but in order to maintain initial object’s aspect ratio, transformation must be exactly calculated with the use of sin and cos.

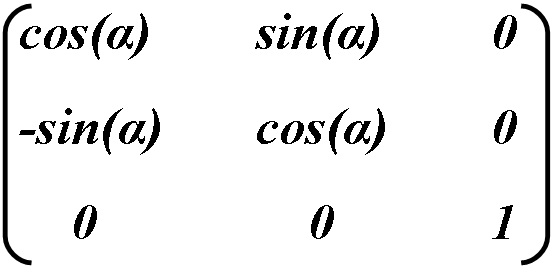
Object is rotated counter-clockwise, α sets rotation angle in rad.

Moving

Moving is preformed by changing following values: e (for horizontal) and f (for vertical). Values are measured in pixels

P.S Matrix is rarely directly used for movement, because this operation can be done with other methods, for example, dragging object with mouse in the workspace.

Since transformation matrix has just 6 elements available for modification, it is visually displayed in PDF as [a b c d e f]. Such matrix can represent any linear transformation from one coordinate system to another. Transformation matrices are formed following way:

Movements are represented as [1 0 0 1 t_x t_y], где t_xи t_y— distances from coordinate axis horizontally and vertically correspondingly.
Scaling is represented as t_y. This scales coordinates so that 1 unit in horizontal and vertical measurements in new coordinate system equals s_x and s_y units in old coordinate systems correspondingly.
Rotations are preformed with matrix [cosθ sinθ −sinθ cosθ 0 0], which matches counter clockwise rotation of all coordinate system by θ rad.
Skew is represented as [1 tanα tanβ 1 0 0], which matches skew of x axis by α angle and axis y by β.

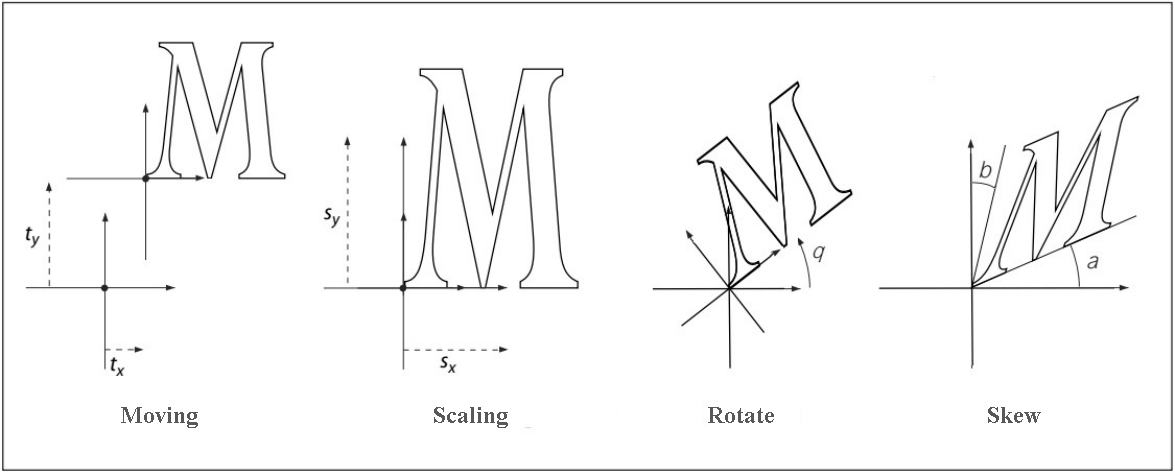
Image below shows transformation samples. Move direction, rotation and skew angles shown on image correspond to positive matrix values.

Matrix multiplications are not commutative, so it makes difference in which order you multiply matrices.

Table below lists possible transformations and corresponding matrix values.

Original picture	Transformed picture	Matrix	Description
		1 0 0 2 0 0	Vertical scale. If changed value > 1, object is stretched, otherwise narrowed.
		2 0 0 1 0 0	Horizontal scale. If changed value > 1, object is stretched, otherwise shrinks.
		-1 0 0 1 0 0	Horizontal mirroring.
		1 0 0 -1 0 0	Vertical mirroring.
		1 1 0 1 0 0	Vertical skew up.
		1 -1 0 1 0 0	Vertical skew down.
		1 0 1 1 0 0	Horizontal skew right.
		1 0 -1 1 0 0	Horizontal skew left.
		1 0 0 1 0 1	Moving up in pixels.
		1 0 0 1 0 -1	Moving down in pixels.
		1 0 0 1 1 0	Moving right in pixels.
		1 0 0 1 -1 0	Moving left in pixels.